Followup to Sorting with Bialgebras

Last week I was pretty down on the results of my exploration into Sorting with Bialgebras. I didn’t want to get into the habit of slamming through a paper just to not understand it, so I figured I’d take a hit on my yearly goal and spend this week getting the results up to snuff.

I started by really trying to wrap my head around how exactly the ana . cata pattern works. So I wrote out a truly massive number of trace statements, and stared at them until they made some amount of sense. Here’s what’s going on:

ana takes an a and unfolds it into an F a, recursively repeating until it terminates by producing a non-inductive F-term. So here F is a Sorted. And then we need to give a folding function for cata. This fold happens in Unsorted, and thus has type Unsorted (Sorted (Mu Unsorted)) -> Sorted (Mu Unsorted). The idea here is that the cata uses its resulting Sorted to pull forward the smallest element it’s seen so far. Once the cata is finished, the ana gets a term Sorted (Mu Unsorted), where the Sorted term is the head of the synthesized list, and the Mu Unsorted is the next “seed” to recurse on. This Mu Unsorted is one element smaller than it was last time around, so the recursion eventually terminates.

OK, so that’s all well and good. But what does ana . para do here? Same idea, except that the fold also gets a Mu Unsorted term, corresponding to the unsorted tail of the list — aka, before it’s been folded by para.

The paper doesn’t have much to say about para:

in a paramorphism, the algebra also gets the remainder of the list. This extra parameter can be seen as a form of an as-pattern and is typically used to match on more than one element at a time or to detect that we have reached the final element.

That’s all well and good, but it’s unclear how this can help us. The difference between naiveIns and ins is:

naiveIns
    :: Ord a
    => Unsorted a (Sorted a x)
    -> Sorted a (Unsorted a x)
naiveIns UNil = SNil
naiveIns (a :> SNil) = a :! UNil
naiveIns (a :> b :! x)
  | a <= b    = a :! b :> x
  | otherwise = b :! a :> x

ins
    :: Ord a
    => Unsorted a (c, Sorted a x)
    -> Sorted a (Either c (Unsorted a x))
ins UNil = SNil
ins (a :> (x, SNil)) = a :! Left x
ins (a :> (x, b :! x'))
  | a <= b    = a :! Left x
  | otherwise = b :! Right (a :> x')

Ignore the Left/Right stuff. The only difference here is whether we use x or x' in the last clause, where x is the original, unsorted tail, and x' is the somewhat-sorted tail. It’s unclear to me how this can possibly help improve performance; we still need to have traversed the entire tail in order to find the smallest element. Maybe there’s something about laziness here, in that we shouldn’t need to rebuild the tail, but we’re going to be sharing the tail-of-tail regardless, so I don’t think this buys us anything.

And this squares with my confusion last week; this “caching” just doesn’t seem to do anything. In fact, the paper doesn’t even say it’s caching. All it has to say about our original naiveIns:

Why have we labelled our insertion sort as naïve? This is because we are not making use of the fact that the incoming list is ordered— compare the types of bub and naiveIns. We will see how to capitalise on the type of naiveIns in Section 5.

and then in section 5:

The sole difference between sel and bub (Section 3) is in the case where a 6 b: sel uses the remainder of the list, supplied by the paramorphism, rather than the result computed so far. This is why para sel is the true selection function, and fold bub is the naïve variant, if you will.

OK, fair, that checks out with what came out of my analysis. The ana . para version does use the tail of the original list, while ana . cata uses the version that might have already done some shuffling. But this is work we needed to do anyway, and moves us closer to a sorted list, so it seems insane to throw it away!

The best argument I can come up with here is that the ana . para version is dual to cata . apo, which signals whether the recursion should stop early. That one sounds genuinely useful to me, so maybe the paper does the ana . para thing just out of elegance.

Unfortunately, cata . apo doesn’t seem to be a performance boost in practice. In fact, both cata . ana and ana . cata perform significantly better than cata . apo and ana . para. Even more dammingly, the latter two perform better when they ignore the unique abilities that apo and para provide.

Some graphs are worth a million words:

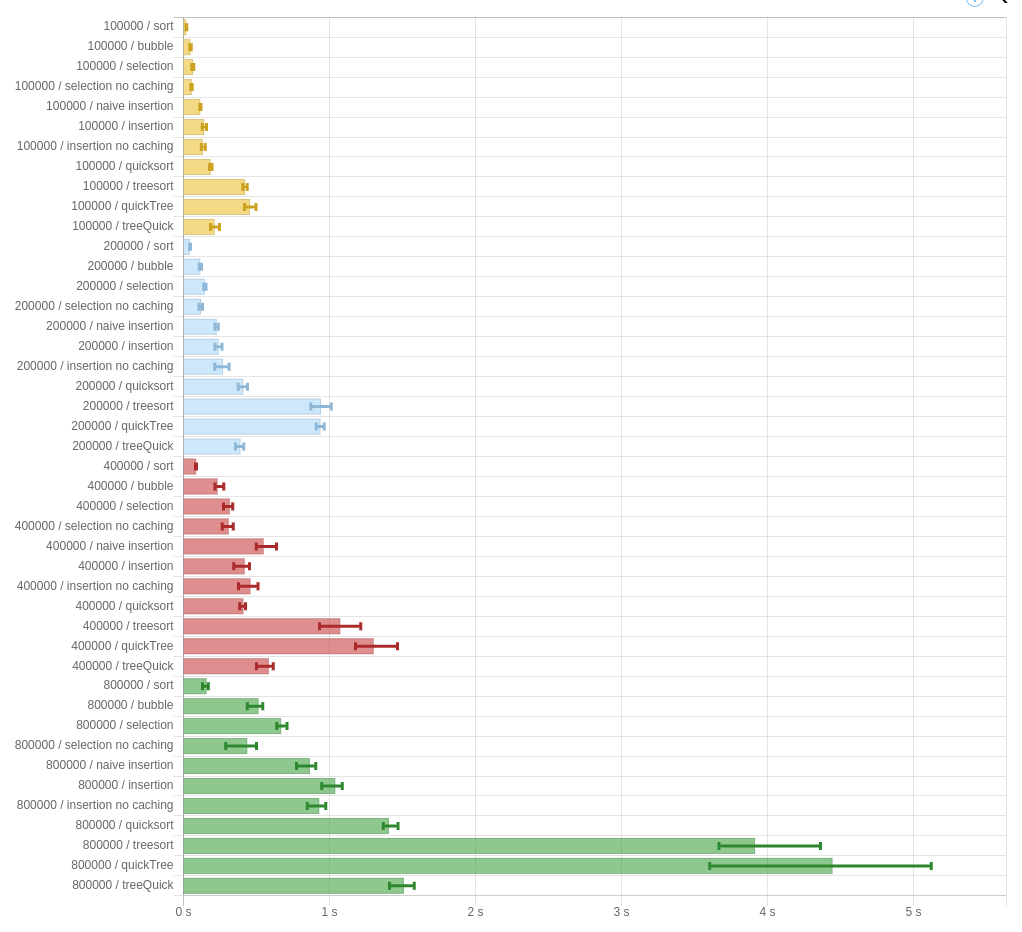
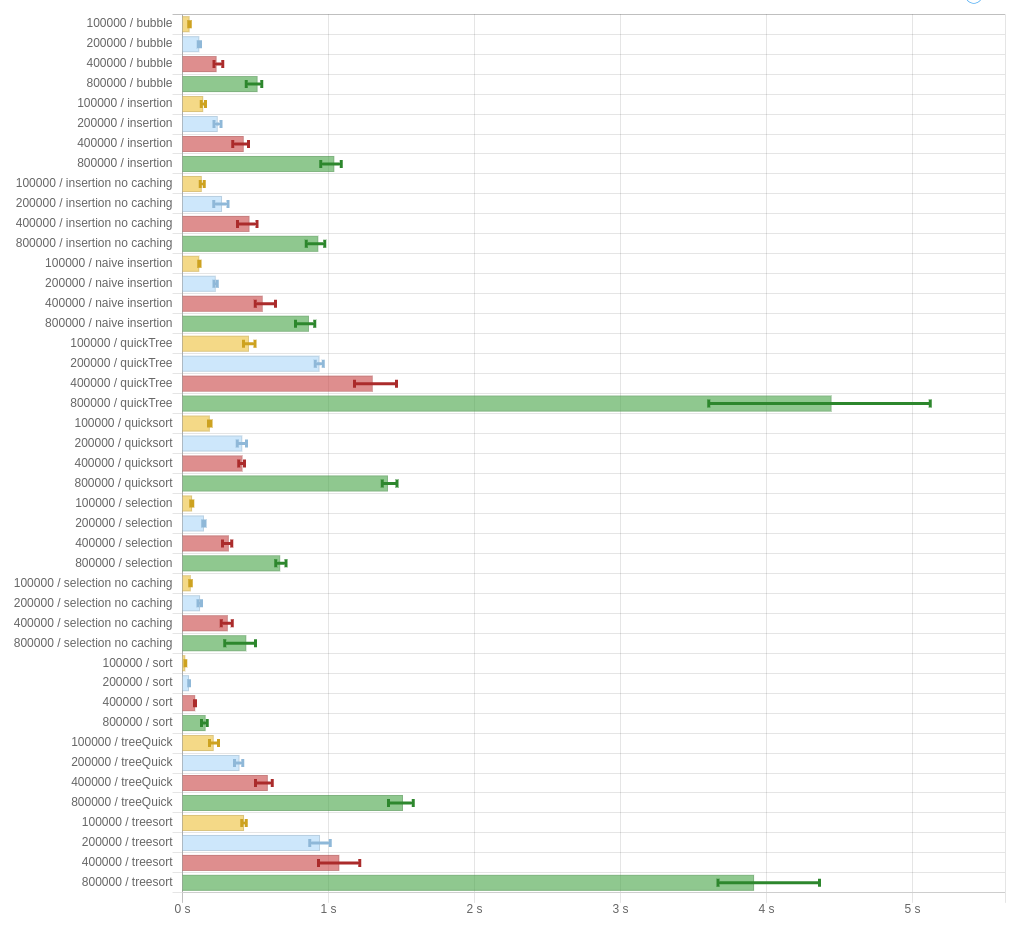
These are performance benchmarks for -00, using Data.List.sort as a control (“sort”). The big numbers on the left are the size of the input. “bubble” is the naive version of “selection.” Additionally, the graphs show the given implementations of quickSort and treeSort, as well as the two variations I was wondering about in the last post (here called quickTree and treeQuick.)

The results are pretty damming. In all cases, bubble-sort is the fastest of the algorithms presented in the paper. That’s, uh, not a good sign.

Furthermore, the “no caching” versions of “insertion” and “selection” both perform better than their caching variants. They are implemented by just ignoring the arguments that we get from apo and para, and simulating being ana and cata respectively. That means: whatever it is that apo and para are doing is strictly worse than not doing it.

Not a good sign.

But maybe this is all just a result of being run on -O0. Let’s try turning on optimizations and seeing what happens:

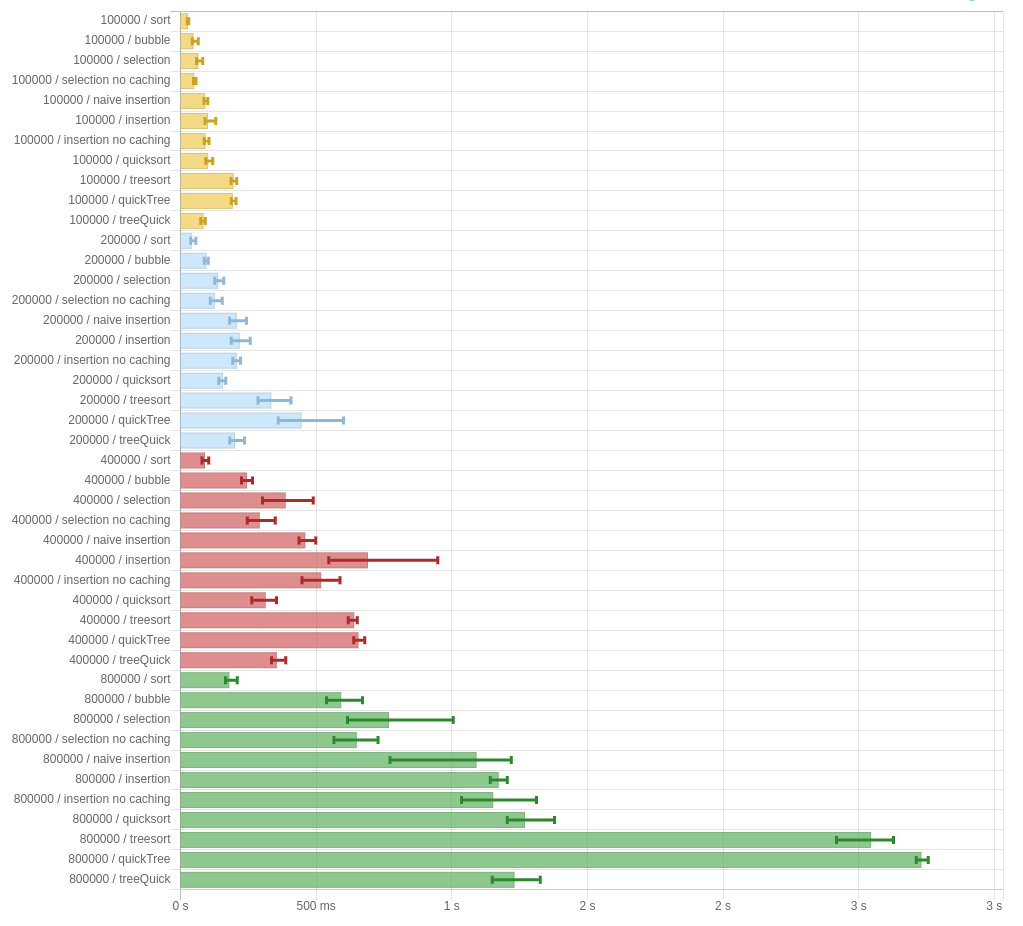
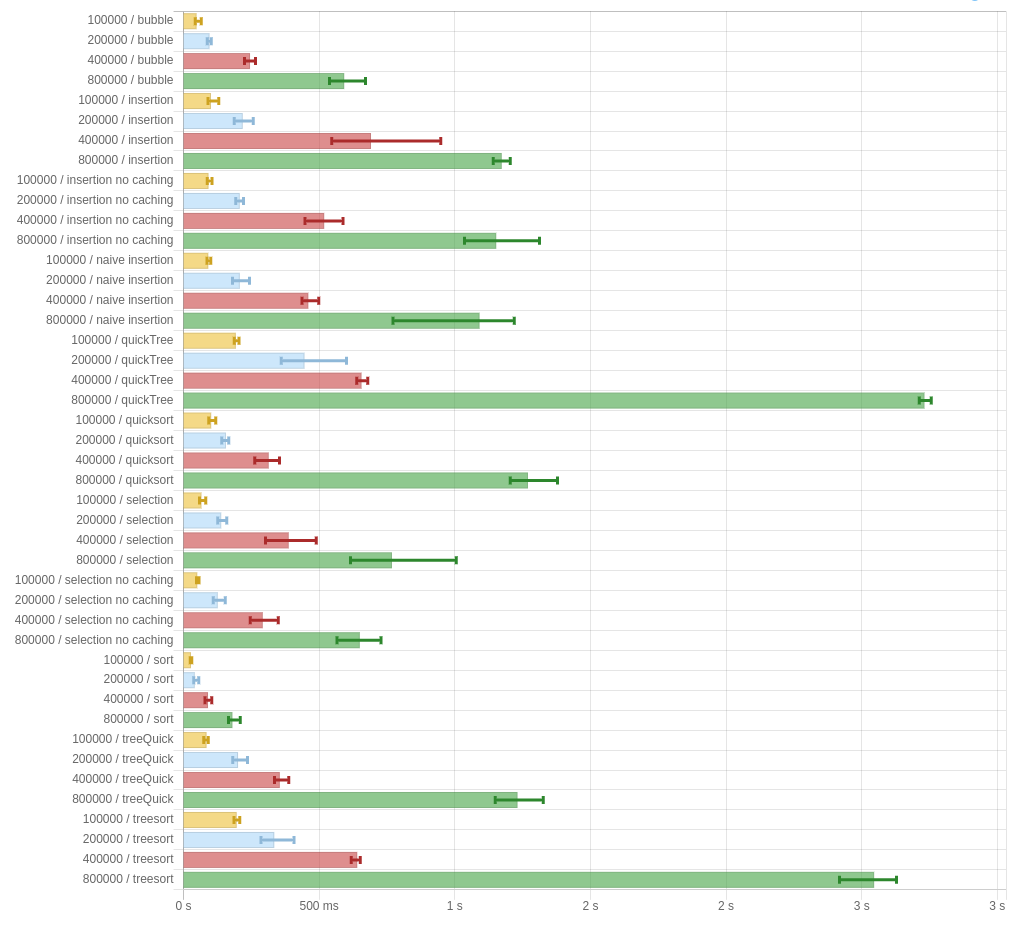
About the same. Uh oh.

I don’t know what to blame this on. Maybe the constant factors are bad, or it’s a runtime thing, or I fucked up something in the implementation, or maybe the paper just doesn’t do what it claims. It’s unclear. But here’s my code, in case you want to take a look and tell me if I screwed something up. The criterion reports are available for -O0 and -O2 (slightly different than in the above photos, since I had to rerun them.)